Table des matières

Lois usuelles à densité

Var densité >	Généralités	Lois usuelles	Transfert	Espérance	Variance

Lois usuelles à densité

Loi uniforme

Théorème : Cas particulier et cas général

Les fonctions $1\!\!1_{[0,1]}\colon x\mapsto\begin{cases} 0 & \text{si}\; x\notin[0,1]\\ 1 & \text{si}\; x\in[0,1] \end{cases}$ et plus généralement $\ds\frac{1}{b-a}1\!\!1_{[a,b]}\colon x\mapsto\begin{cases} 0 & \text{si}\; x\notin[a,b]\\ \ds\frac{1}{b-a} & \text{si}\; x\in[a,b] \end{cases}$ pour $(a,b)\in\R^{2}$ avec $a<b$ sont des densités de probabilité.

Définition

On dit qu'une variable aléatoire $X$ suit la loi uniforme sur un intervalle $[a,b]$ (avec $(a,b)\in\R^{2}$ et $a<b$) si et seulement si l'une de ses densités est la fonction $\ds\frac{1}{b-a}1\!\!1_{[a,b]}$ et on note alors : $X\hookrightarrow\mathcal{U}([a,b])$.

Remarques

Les fonctions $1\!\!1_{[a,b[}$, $1\!\!1_{]a,b]}$ et $1\!\!1_{]a,b[}$ sont aussi des densités de $X\hookrightarrow\mathcal{U}([a,b])$.
On admet que la fonction rand() du langage Scilab suit approximativement la loi $\mathcal{U}([0,1])$.
La fonction grand(n,p,“unf”,a,b) du langage Scilab produit une matrice de $\mathcal{M}_{n,p}(\R)$ dont les éléments sont des réalisations de la loi $\mathcal{U}([a,b])$.

Théorème : Fonction de répartition

Les fonctions de répartition de $X\hookrightarrow\mathcal{U}([0,1])$ et $Y\hookrightarrow\mathcal{U}([a,b])$ (avec $(a,b)\in\R^{2}$ et $a<b$) sont :
$$\ds\forall x\in\R,\qquad F_{X}(x)=\begin{cases} 0 & \text{si}\; x<0\\ x & \text{si}\;0\leqslant x\leqslant1\\ 1 & \text{si}\; x>1 \end{cases}\qquad F_{Y}(x)=\begin{cases} 0 & \text{si}\; x<a\\ \ds\frac{x-a}{b-a} & \text{si}\; a\leqslant x\leqslant b\\ 1 & \text{si}\; x>b \end{cases}$$

Loi exponentielle

Théorème : Cas particulier et cas général

Les fonctions $x\mapsto\mathrm{e}^{-x}1\!\!1_{[0,+\infty[}(x)=\begin{cases} 0 & \text{si}\; x<0\\ \mathrm{e}^{-x} & \text{si}\; x\geqslant0 \end{cases}$ et plus généralement $x\mapsto\lambda\mathrm{e}^{-\lambda x}1\!\!1_{[0,+\infty[}(x)=\begin{cases} 0 & \text{si}\; x<0\\ \lambda\mathrm{e}^{-\lambda x} & \text{si}\; x\geqslant0 \end{cases}$ pour $\lambda\in\left]0,+\infty\right[$ sont des densités de probabilité.

Définition

On dit que qu'une variable aléatoire $X$ suit la loi exponentielle de paramètre $\lambda$ (avec $\lambda>0$) si et seulement si l'une de ses densités est la fonction $x\mapsto\lambda\mathrm{e}^{-\lambda x}1\!\!1_{[0,+\infty[}(x)$, ce que l'on note : $X\hookrightarrow\mathcal{E}(\lambda)$.

Théorème : Fonction de répartition

Les fonctions de répartition de $X\hookrightarrow\mathcal{E}(1)$ et $Y\hookrightarrow\mathcal{E}(\lambda)$ (avec $\lambda>0$) sont :
$$\forall x\in\R,\qquad F_{X}(x)=\begin{cases} 0 & \text{si}\; x<0\\ 1-\mathrm{e}^{-x} & \text{si}\; x\geqslant0 \end{cases}\qquad F_{Y}(x)=\begin{cases} 0 & \text{si}\; x<0\\ 1-\mathrm{e}^{-\lambda x} & \text{si}\; x\geqslant0 \end{cases}$$

Exemple

// lois exponentielles
function y=f(t)
    y=lambda*exp(-lambda*t)
endfunction
function y=F(t)
    y=1-exp(-lambda*t)
endfunction
x=[0:0.01:5]
k=0
for lambda=[0.5,1,2]
    k=k+1
    subplot(2,3,k) ; fplot2d(x,f,5)
    subplot(2,3,k+3) ; fplot2d(x,F,5)
end

loi_exponentielle.pdf

Remarque

La fonction grand(n,p,“exp”,1/lambda) du langage Scilab produit une matrice de $\mathcal{M}_{n,p}(\R)$ dont les éléments sont des réalisations de la loi $\mathcal{E}(\lambda)$.

Exemple

Soit $m\in\R$. Soit $X\hookrightarrow\mathcal{E}(\lambda)$ où $\lambda>0$. Déterminer la loi de $Y=\max(X,m)$. À-t-on une variable à densité ?

Définition

Soit $X$ une variable aléatoire à valeurs positives et telle que :
$$\ds\forall x\geqslant0,\;\mathbb{P}(X>x)>0$$On dit que la loi de $X$ est une loi sans mémoire si et seulement si :
$$\ds\forall(x,y)\in\left[0,+\infty\right[^{2},\;\mathbb{P}_{[X>y]}(X>x+y)=\mathbb{P}(X>x)$$

Remarques

Si $X$ mesure la durée de vie d'une machine alors l'absence de mémoire (l'absence de vieillissement ici) signifie que sa probabilité de fonctionner encore $x$ unités de temps sachant qu'elle a déjà fonctionné $y$ unités de temps est la même que sa probabilité de fonctionner $x$ unités de temps dès après sa fabrication.
Remarquons aussi que la propriété d'absence de mémoire est équivalente aux deux propositions suivantes : $$\ds\forall(x,y)\in\left[0,+\infty\right[^{2},\;\mathbb{P}(X>x+y)=\mathbb{P}(X>x)\mathbb{P}(X>y)$$ $$\ds\forall(x,y)\in\left[0,+\infty\right[^{2},\; F_{X}(x+y)=F_{X}(x)+F_{X}(y)-F_{X}(x)F_{X}(y)$$

Théorème : Caractérisation d'une loi sans mémoire à densité

Soit $X$ une variable aléatoire à densité, à valeurs positives et telle que $\mathbb{P}(X>x)>0$ pour tout réel $x\geqslant0$. Alors, la loi de $X$ est une loi sans mémoire si et seulement si $X$ suit une loi exponentielle.

Loi gamma

Théorème

Pour tout réel $\nu>0$, la fonction $t\mapsto\begin{cases} 0 & \text{si}\; t\leqslant0\\ \ds\frac{1}{\Gamma(\nu)}t^{\nu-1}\mathrm{e}^{-t} & \text{si}\; t>0 \end{cases}$ est une densité de probabilité.

Définition

Soit $\nu$ un réel strictement positif. On dit qu'une variable aléatoire $X$ suit la loi gamma de paramètre $\nu$ si et seulement si l'une de ses densités est la fonction $t\mapsto\begin{cases} 0 & \text{si}\; t\leqslant0\\ \ds\frac{1}{\Gamma(\nu)}t^{\nu-1}\mathrm{e}^{-t} & \text{si}\; t>0 \end{cases}$ et on note alors : $X\hookrightarrow\gamma(\nu)$.

Remarques

On ne peut pas déterminer une expression de la fonction de répartition de la loi $\gamma(\nu)$ mis à part dans le cas où $\nu\in\N^{*}$ en procédant des intégrations par parties successives.
La fonction grand(n,p,“gam”,nu,1) du langage Scilab produit une matrice de $\mathcal{M}_{n,p}(\R)$ dont les éléments sont des réalisations de la loi $\gamma(\nu)$.

Exemples

Justifier que $\gamma(1)=\mathcal{E}(1)$.
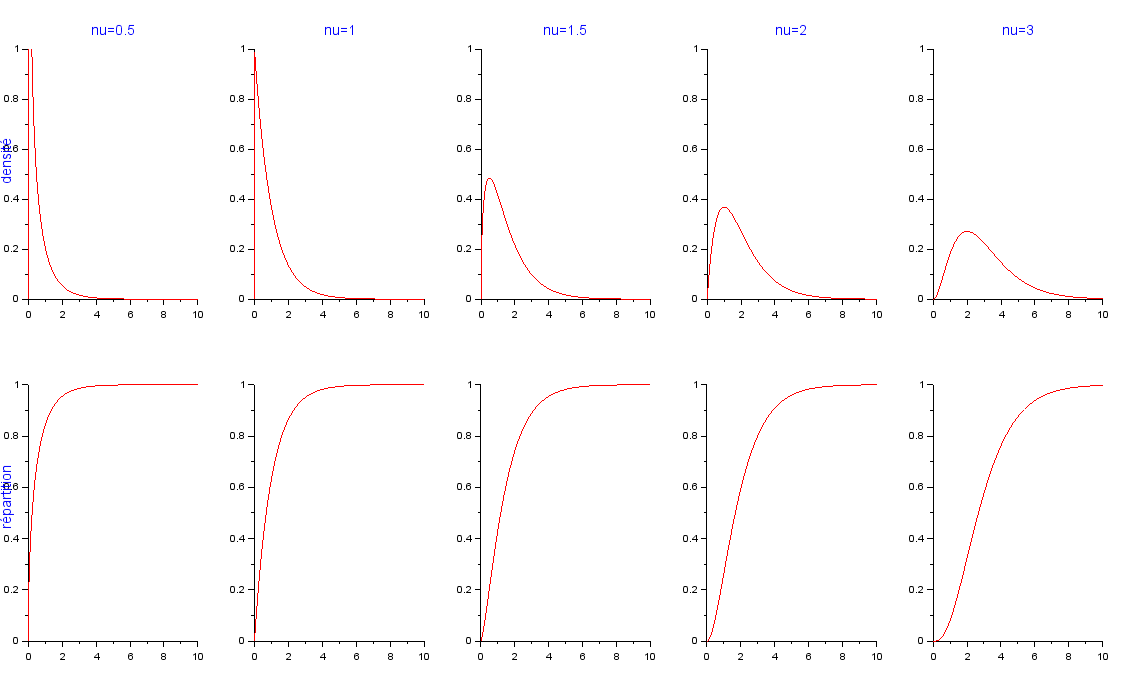
Tracer l'allure d'une densité puis de la répartition de $\ds\gamma\left(\frac{1}{2}\right),\gamma(1),\gamma\left(\frac{3}{2}\right),\gamma(2),\gamma(3)$.

// lois gamma
function y=f(t)
    if t>0
        y=1/gamma(nu)*t^(nu-1)*exp(-t)
    else
        y=0
    end
endfunction
x=[0:0.01:10]
k=0
for nu=[0.5,1,1.5,2,3]
    k=k+1
    subplot(2,5,k) ; fplot2d(x,f,5)
    [y,z]=cdfgam("PQ",x,nu*ones(x),ones(x))
    subplot(2,5,k+5) ; plot2d(x,y,5)
end

loi_gamma.pdf

Loi normale

Remarques

On admet que : $$\ds\int_{-\infty}^{+\infty}{\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^{2}}{2}}\mathrm{d} x}=1$$
On en déduit que : $$\ds\Gamma\left(\frac{1}{2}\right)=\int_{0}^{+\infty}{\frac{\mathrm{e}^{-t}}{\sqrt{t}}\mathrm{d} t}=\sqrt{\pi}$$

Théorème

La fonction $\ds\varphi\colon x\mapsto\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^{2}}{2}}$ est une densité de probabilité.

Définition

On dit qu'une variable aléatoire $X$ suit la loi normale centrée réduite (ou encore loi de Gauss) si et seulement si l'une de ses densités est la fonction $\ds x\mapsto\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^{2}}{2}}$ (souvent notée $\varphi$) et on note : $X\hookrightarrow\mathcal{N}(0,1)$.
La fonction de répartition $F_{X}$ de $X$ est souvent notée $\Phi$ : $$\ds\forall x\in\R,\;\Phi(x)=\mathbb{P}(X\leqslant x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}{\mathrm{e}^{-\frac{t^{2}}{2}}\mathrm{d} t}$$

Remarque

On ne peut exprimer la fonction de répartition $\Phi$ sans l'aide d'une intégrale. Pour des calculs numériques, on utilise une table de valeur comme ci-dessous : Étudier puis représenter les fonctions $\varphi$ et $\Phi$. Préciser les points d'inflexion.

Théorème : Propriété fondamentale de la fonction de répartition Φ

Soit $X\hookrightarrow\mathcal{N}(0,1)$. Alors : $$\ds\forall x\in\R,\;\Phi(-x)=1-\Phi(x)$$

Exemples

Calculer $\mathbb{P}(X\leqslant0)$.
Lectures de la table de valeurs.
1. Déterminer une valeur approchée de $\mathbb{P}(2\leqslant X\leqslant3)$ puis de $\mathbb{P}(-3\leqslant X\leqslant1)$.
2. Déterminer une valeur approchée de : $\mathbb{P}(-1\leqslant X\leqslant1)$, $\mathbb{P}(-2\leqslant X\leqslant2)$ et $\mathbb{P}(-3\leqslant X\leqslant3)$.

Théorème

Pour tout réel $m$ et tout réel $\sigma>0$, la fonction $\ds x\mapsto\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^{2}}{2\sigma^{2}}\right)$ est une densité de probabilité.

Définition

Soit $m$ un réel et $\sigma$ un réel strictement positif. On dit qu'une variable aléatoire $X$ suit la loi normale (ou loi de Gauss-Laplace) de paramètre $(m,\sigma^{2})$ si et seulement si l'une de ses densités est la fonction $\ds x\mapsto\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^{2}}{2\sigma^{2}}\right)$ et on note : $X\hookrightarrow\mathcal{N}(m,\sigma^{2})$.

Exemples à m constant et sigma variable

function p=normal(t,m,s)
    p=exp(-(t-m)^2/2/s^2)/sqrt(2*%pi*s^2)
endfunction
n=5
m=10
s=[1:n]
x=[-5:0.001:25]' 
y=zeros(x*s) ; z=zeros(y)
for k=[1:n]
    y(:,k)=cdfnor("PQ",x,m*ones(x),s(k)*ones(x))
    for i=[1:length(x)]
        z(i,k)=normal(x(i),m,s(k))
    end
end
subplot(2,1,1) ; plot2d(x,y) ; plot2d([0,m],[0.5,0.5]) ; plot2d([m,m],[0,0.5])
subplot(2,1,2) ; plot2d(x,z) ; plot2d([m,m],[0,0.4])

Var densité >	Généralités	Lois usuelles	Transfert	Espérance	Variance