Proj/Sym >	Généralités	Proj ortho	Minimalisation

Projections orthogonales

Définition

Soit $E$ un espace euclidien. On appelle projection orthogonale sur un sous-espace vectoriel $F$, notée $p_{F}$, la projection sur $F$ parallèlement à $F^{\perp}$.

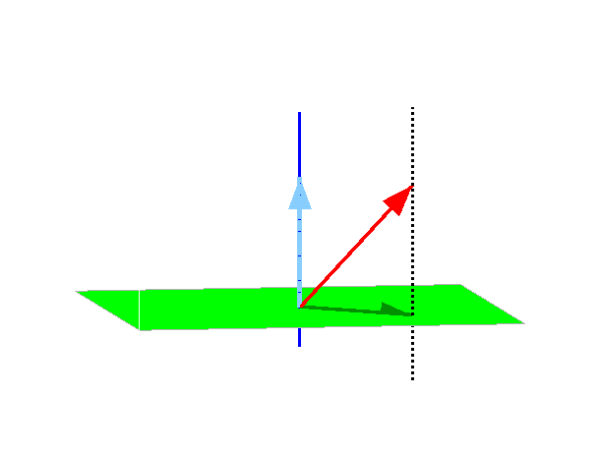
// plan P de projection
// P=Vect(i,j)
plot3d([-1,1],[-1,1],[0,0;0,0])
// droite D de direction de projection
// D=Vect(k) avec u=(0,0,1)=0.i+0.j+1.k
u=[0,0,3]
t=[-0.2,1] ; param3d(t*u(1),t*u(2),t*u(3))
// vecteur x à projeter sur P parallèlement à D
// x=(-1/2,1/2,1/2)=(-1/2).i+1/2.j+1/2.k
x=[-1/2,1/2,2]
t=[0,1] ; param3d(t*x(1),t*x(2),t*x(3))
// vecteurs xP et xD
param3d(t*x(1),t*x(2),t*0)
param3d(t*0,t*0,t*x(3))
// trace pour règle du parallélogramme
t=[-1,0.4]
param3d(x(1)+t*u(1),x(2)+t*u(2),x(3)+t*u(3))

Exemples

Soit $p$ un projecteur de $E$. Montrer que $p$ est un projecteur orthogonal si et seulement si $\text{Ker}(p)\perp\text{Im}(p)$.
Dans $\R^{3}$ muni du produit scalaire canonique, on considère le plan $P$ d'équation $x+2y+3z=0$. Déterminer la matrice de la projection orthogonale sur $P$ dans la base canonique de $\R^{3}$.

Théorème : Coordonnées du projeté orthogonal

Soit $E$ un espace euclidien et $F$ un sous-espace de $E$.

Soit $(\vv{u_1},\dots,\vv{u_m})$ une base orthonormale de $F$, sous-espace de $E$. Alors : $$\ds\forall\vv{x}\in E,\; p_{F}(\vv{x})=\sum_{k=1}^{m}{\left\langle x,\vv{u_k}\right\rangle \vv{u_k}}$$
Soit $\mathcal{B}=(\vv{e_1},\dots,\vv{e_n})$ une base orthonormale de $E$. On note $U_{1},\dots,U_{m}$ les colonnes de coordonnées des vecteurs $\vv{u_1},\dots,\vv{u_m}$ dans la base $\mathcal{B}$. Alors : $$\ds\text{Mat}_{\mathcal{B}}(p_{F})=\sum_{i=1}^{m}{U_{i}{}^{t}U_{i}}$$

Exemple

On considère l'espace vectoriel $\R_{3}[X]$ muni du produit scalaire : $$\ds\left\langle P,Q\right\rangle =\int_{0}^{1}{P(t)Q(t)\mathrm{d} t}$$ On pose : $F=\text{Vect}(1,X)$. Déterminer $p_{F}(1+X+X^{2}+X^{3})$.

Proj/Sym >	Généralités	Proj ortho	Minimalisation