Table des matières
Convergence en loi et approximations de certaines lois usuelles
Définition et propriétés
Définition
On dit que la suite de variables aléatoires $(X_{n})_{n\in\N}$ converge en loi vers la variable aléatoire $X$ et on note $X_{n}\xrightarrow{\mathcal{L}}X$ si et seulement si :
$$\ds\forall x\in\mathcal{D}_{X},\;\lim_{n\to+\infty}{F_{X_{n}}(x)}=F_{X}(x)$$où $\mathcal{D}_{X}$ désigne l'ensemble des points de continuité de la fonction de répartition $F_{X}$ de $X$.
Exemples
- On suppose que $\ds X_{n}\hookrightarrow\mathcal{U}\left(\left\{ \frac{1}{n},\frac{2}{n},\dots,\frac{n-1}{n},\frac{n}{n}\right\} \right)$ pour tout entier $n\geqslant1$. Montrer que $X_{n}\xrightarrow{\mathcal{L}}X$ où $X\hookrightarrow\mathcal{U}([0,1])$.
plot2d([-0.5,0],[0,0],5) for n=[1,2,5,10,20,50,100] x=[0:1/n:1] for k=[1:n] ; plot2d([x(k),x(k+1)],[x(k),x(k)],2+floor(2*log(n))) ; end end plot2d([1,1.5],[1,1],5)
- On suppose que $\ds X_{n}\hookrightarrow\mathcal{U}\left(\left\{ \frac{1}{n}\right\} \right)$ pour tout entier $n\geqslant1$. Montrer que $X_{n}\xrightarrow{\mathcal{L}}01\!\!1_{\Omega}$.
- On suppose que $\ds U_{n}\hookrightarrow\mathcal{U}\left(\left[0,1\right]\right)$ pour tout entier $n\geqslant1$ et que ces variables aléatoires sont mutuellement indépendantes. Pour tout entier $n\geqslant1$, on pose :
$$M_{n}=\max(U_{1},\dots,U_{n})$$et :
$$X_{n}=n(1-M_{n})$$Montrer que $X_{n}\xrightarrow{\mathcal{L}}X$ où l'on a $X\hookrightarrow\mathcal{E}(1)$.
Remarques
- La convergence en loi est une convergence basée sur la « convergence simple » des fonctions de répartitions. Rien n'oblige donc à avoir $X_{n}(\omega)\xrightarrow[n\to+\infty]{}X(\omega)$ pour ne serait-ce qu'un élément $\omega$ de $\Omega$ (considérer $\ds X_{n}=X\hookrightarrow\mathcal{B}\left(1,\frac{1}{2}\right)$ et $Y=1-X$ qui donne $X_{n}\xrightarrow{\mathcal{L}}Y$).
- Une notation qui pourrait être plus évocatrice de cette convergence :
$$\ds\mathcal{L}(X_{n})\xrightarrow[n\to+\infty]{}\mathcal{L}(X)$$ - Une suite de variables aléatoires discrètes peut converger en loi vers une variable aléatoire discrète ou bien une variable aléatoire à densité.
- Une suite de variables aléatoires à densité peut converger en loi vers une variable aléatoire à densité ou bien une variable aléatoire discrète.
- L'exemple 2 « justifie », à quelques détails près, que la fonction rand() du langage SciLab est une bonne approximation de la loi uniforme sur $[0,1[$ : les résultats fournis par cette fonction sont obtenus avec des probabilités semblables à ceux qui auraient été fournis par une vraie variable aléatoire suivant la loi $\mathcal{U}([0,1[)$.
Théorème : Lien entre les deux notions de convergence (HP)
Si $X_{n}\xrightarrow{\mathbb{P}}X$ alors $X_{n}\xrightarrow{\mathcal{L}}X$. La réciproque est fausse.
Exemple et contre exemple
- Soit $U\hookrightarrow\mathcal{U}([0,1])$ et $(U_{n})_{n\geqslant1}$ une suite de variables aléatoires mutuellement indépendantes ayant toutes la même loi que $U$. Pour tout entier naturel $n$ non nul, on pose :
$$S_{n}=\sup(U_{1},\dots,U_{n})$$Montrer que $S_{n}\xrightarrow{\mathcal{P}}1$ puis que $S_{n}\xrightarrow{\mathcal{L}}1$. - Soit $\ds X\hookrightarrow\mathcal{B}\left(1,\frac{1}{2}\right)$, $Y=1-X$ et $X_{n}=X$ pour tout entier naturel $n$.
- Justifier que $\ds Y\hookrightarrow\mathcal{B}\left(1,\frac{1}{2}\right)$ puis que la suite $(X_{n})_{n\geqslant0}$ converge en loi vers $Y$.
- Montrer que :
$$\forall n\in\N,\;|X_{n}-Y|=|1-2X|=1\!\!1_{\Omega}$$ - En déduire que, pour tout réel $\varepsilon\in\left]0,1\right[$, on a :
$$\ds\mathbb{P}\left(|X_{n}-Y|>\varepsilon\right)=\mathbb{P}\left(|1\!\!1_{\Omega}>\varepsilon\right)=1$$ - Conclure.
Remarques
- La convergence en loi est plus faible (moins contraignante) que la convergence en probabilité.
- Il n'y a pas unicité de la limite lors de la convergence en loi.
- Il n'y a pas compatibilité de l'espérance avec la convergence en loi.
- La convergence en loi n'est pas compatible, sauf cas particuliers ci-après, avec les opérations sur les variables aléatoires.
Exemples
- Pour tout entier $n\geqslant1$, on considère la variable aléatoire $X_{n}$ dont la loi est :
$$\ds\left\{ \left(\frac{1}{n},1-\frac{1}{n}\right),\left(n,\frac{1}{n}\right)\right\}$$Justifier que :
$$\ds X_{n}\xrightarrow{\mathcal{L}}0$$ puis calculer $\mathbb{E}(X_{n})$. - Soit $\ds X\hookrightarrow\mathcal{B}\left(1,\frac{1}{2}\right)$, $Y=1-X$, $X_{n}=X$ et $Y_{n}=1-X_{n}$ pour tout entier naturel $n$.
- Justifier que $(X_{n})$ et $(Y_{n})$ convergent toutes les deux en loi vers $X$.
- Justifier que $(X_{n}+Y_{n})$ ne converge pas en loi vers $X+X=2X$.
Théorème (admis)
Si $X_{n}\xrightarrow{\mathcal{L}}X$ et si $f\colon\R\to\R$ est continue sur $\R$ alors $f(X_{n})\xrightarrow{\mathcal{L}}f(X)$.
Théorème : Théorème de Slutsky (admis)
Si $X_{n}\xrightarrow{\mathcal{L}}X$ et $Y_{n}\xrightarrow{\mathcal{P}}c1\!\!1_{\Omega}$ (convergence en loi pour la première suite, en probabilité pour la seconde) alors :
$$\ds X_{n}+Y_{n}\xrightarrow{\mathcal{L}}X+c$$et :
$$\ds X_{n}Y_{n}\xrightarrow{\mathcal{L}}cX$$
Cas des variables discrètes à valeurs dans Z
<html><a name=“convergence_loi_variables_valeurs_dans_z”></a></html>
- Soit $(X_{n})_{n\in\N}$ une suite de variables aléatoires à valeurs dans $\Z$ et $X$ une variable aléatoire à valeurs dans $\Z$. Alors :
$$\ds X_{n}\xrightarrow{\mathcal{L}}X\;\iff\;\forall k\in\Z,\;\lim_{n\to+\infty}{\mathbb{P}(X_{n}=k})=\mathbb{P}(X=k)$$ - En conséquence, si $(X_{n})_{n\in\N}$ est une suite de variables aléatoires à valeurs dans $\N$, si pour tout entier $k\in\N$ la suite $(\mathbb{P}(X_{n}=k))_{n\in\N}$ converge et a pour limite un réel $p_{k}$ et si la série $\ds\sum_{k\geqslant0}{p_{k}}$ converge et sa somme vaut 1 alors la suite $(X_{n})_{n\in\N}$ converge en loi vers une variable aléatoire $X$ dont la loi est donnée par :
$$\ds\forall k\in\N,\;\mathbb{P}(X=k)=p_{k}$$
<html><a name=“approximation_loi_binomiale_par_loi_poisson”></a></html>
Théorème : Approximation 1
- Soit $\lambda>0$. Pour tout entier naturel $n>\lambda$, on considère une variable aléatoire $X_{n}$ suivant la loi $\ds\mathcal{B}\left(n,\frac{\lambda}{n}\right)$. Soit $X$ une variable aléatoire suivant la loi $\mathcal{P}(\lambda)$. Alors :
$$\ds X_{n}\xrightarrow{\mathcal{L}}X$$ - Conditions pratiques d'approximation de lois d'une loi binomiale par une loi de Poisson.
Cette convergence en loi s'interprète de la manière manière suivante : lorsque $n$ est « assez grand » (et donc $\ds\frac{\lambda}{n}$ est « assez petit ») et pour tout entier naturel $k$, on peut écrire :
$$\ds\mathbb{P}\left(X_{n}=k\right)\approx\mathbb{P}\left(X=k\right)$$autrement dit, lorsque $n$ est « grand » et $p$ est « petit », on peut approcher une loi binomiale par une loi de Poisson. En pratique, dès lors que :
$$\boxed{n\geqslant30}\qquad\boxed{p\leqslant0,1}\qquad\boxed{np<15}$$on peut approcher $X\hookrightarrow\mathcal{B}(n,p)$ par $Y\hookrightarrow\mathcal{P}(np)$.
// Convergence en loi d'une loi binomiale vers une loi de Poisson lambda=input("Donner le paramètre lambda : ") for k=1:10 n=10*k bin=[binomial(lambda/n,n) zeros(1,101-n)] ; bin=bin(1:31) poi=[0:30] ; poi=exp(-lambda)*(lambda.^poi)./gamma(poi+1) subplot(5,2,k) ; bar([0:30]',[bin;poi]') end
Cas $\lambda=10$ avec $n\in\{10,20,30,40,50,60,70,80,90,100\}$

Cas $\lambda=5$ avec $n\in\{10,20,30,40,50,60,70,80,90,100\}$

Exemple
Un pisciculteur possède, dans un même bassin, 1000 saumons et 9000 truites. Il attrape successivement et avec remise 100 poissons. Soit $X$ le nombre de saumons pêchés.
- Déterminer la valeur exacte de $\mathbb{P}(X=10)$. Valeur numérique approchée ?
- En utilisant une approximation, déterminer une valeur approchée de $\mathbb{P}(X=10)$. Valeur numérique approchée ?
Remarque
Bien qu'une loi de Poisson ne corresponde à aucune expérience aléatoire élémentaire, elle correspond en fait à une loi limite que l'on retrouve dans de nombreuse situations d'où son importance.
Théorème de la limite centrée et nouvelles approximations
<html><a name=“theoreme_limite_centree”></a></html>
Théorème : Théorème de la limite centrée (admis, “preuve” dans un cas particulier)
On suppose que les $X_{n}$ sont mutuellement indépendantes, admettent la même loi et que cette loi admet une espérance $m$ et une variance $\sigma^{2}$ non nulle ($\sigma>0$). Soit $X\hookrightarrow\mathcal{N}(0,1)$ de fonction de répartition $\Phi$. On pose : $$\ds\forall n\in\N^{*},\;\bar{X}_{n}=\frac{1}{n}\left(X_{1}+\dots+X_{n}\right)$$ $$\ds\bar{X}_{n}^{*}=\sqrt{n}\frac{\bar{X}_{n}-m}{\sigma}$$ Alors, la suite $\ds\left(\bar{X}_{n}^{*}\right)_{n\geqslant1}$ converge en loi vers la variable aléatoire $X$. Autrement dit, on a : $$\ds\forall x\in\R,\;\lim_{n\to+\infty}{F_{\bar{X}_{n}^{*}}(x)}=\Phi(x)$$ ou encore, pour tout couple $(a,b)$ de réels tel que $a<b$, on a :
$$\ds \lim_{n\to+\infty}{\mathbb{P}\left(a\leqslant\bar{X}_{n}^{*}\leqslant b\right)}=\Phi(b)-\Phi(a)=\int_{a}^{b}{\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{t^{2}}{2}}\mathrm{d} t}$$
# Loi faible des grands nombres et théorème central limite # sur une suite de variables de Bernoulli iid import numpy as np ; import numpy.random as rd import matplotlib.pyplot as plt p=0.4 ; N=10**5 ; K=np.arange(1,5) ; a=np.size(K) for k in K : n=10**k ; X=rd.binomial(1,p,size=(N,n)) Xbarre=np.mean(X,axis=1) plt.subplot(a,2,2*k-1) ; plt.hist(Xbarre,np.arange(0,1,0.005)) XbarreEtoile=(Xbarre-p)/np.sqrt(p*(1-p))*np.sqrt(n) x=np.arange(-3,3,0.01) plt.subplot(a,2,2*k) ; plt.hist(XbarreEtoile,x) plt.show()
// Comparatif des répartitions : // loi N(0,1) // somme centrée réduite de lois E(lambda) // somme centrée réduite de lois G(p) n=input("n=") ; lambda=input("lambda=") ; p=input("p=") m=10000 ; Y=zeros(1,m) ; Z=zeros(1,m) for k=1:m X=grand(1,n,"exp",1/lambda) Y(k)=sqrt(n)*(mean(X)-1/lambda)*lambda X=grand(1,n,"geom",p) Z(k)=sqrt(n)*(mean(X)-1/p)/(sqrt(1-p)/p) end abscisses=[-5:0.1:5]' FY=zeros(abscisses) ; FZ=zeros(abscisses) [Phi,Psi]=cdfnor("PQ",abscisses,zeros(abscisses),ones(abscisses)) for k=1:length(abscisses) FY(k)=length(find(Y<=abscisses(k)))/m FZ(k)=length(find(Z<=abscisses(k)))/m end plot2d(abscisses,[FY,FZ,Phi],[5,2,3]) // 5->rouge, 2->bleu 3->vert



// comparatif de convergence entre // - loi faible des grands nombres (bleu) --> valeur de la limite // - théorème de la limite centrée (rouge) --> étalement des résultats autour de la limite // pour une même suite de loi exponentielles de paramètre 1 N=1d4 ; nmax=1d3 ; m=1 ; s=1 X=grand(N,nmax,"exp",m) liste_n=[5,10,20,50,100,nmax] r=length(liste_n) for i=1:r n=liste_n(i) Z=mean(X(:,1:n),'c') Y=(Z-m)/s*sqrt(n) subplot(2,r,i) histplot([-5:0.01:5],Y,5,leg="X"+string(n)+"Barre*") subplot(2,r,i+r) histplot([-5:0.01:5],Z,2,leg="X"+string(n)+"Barre") end
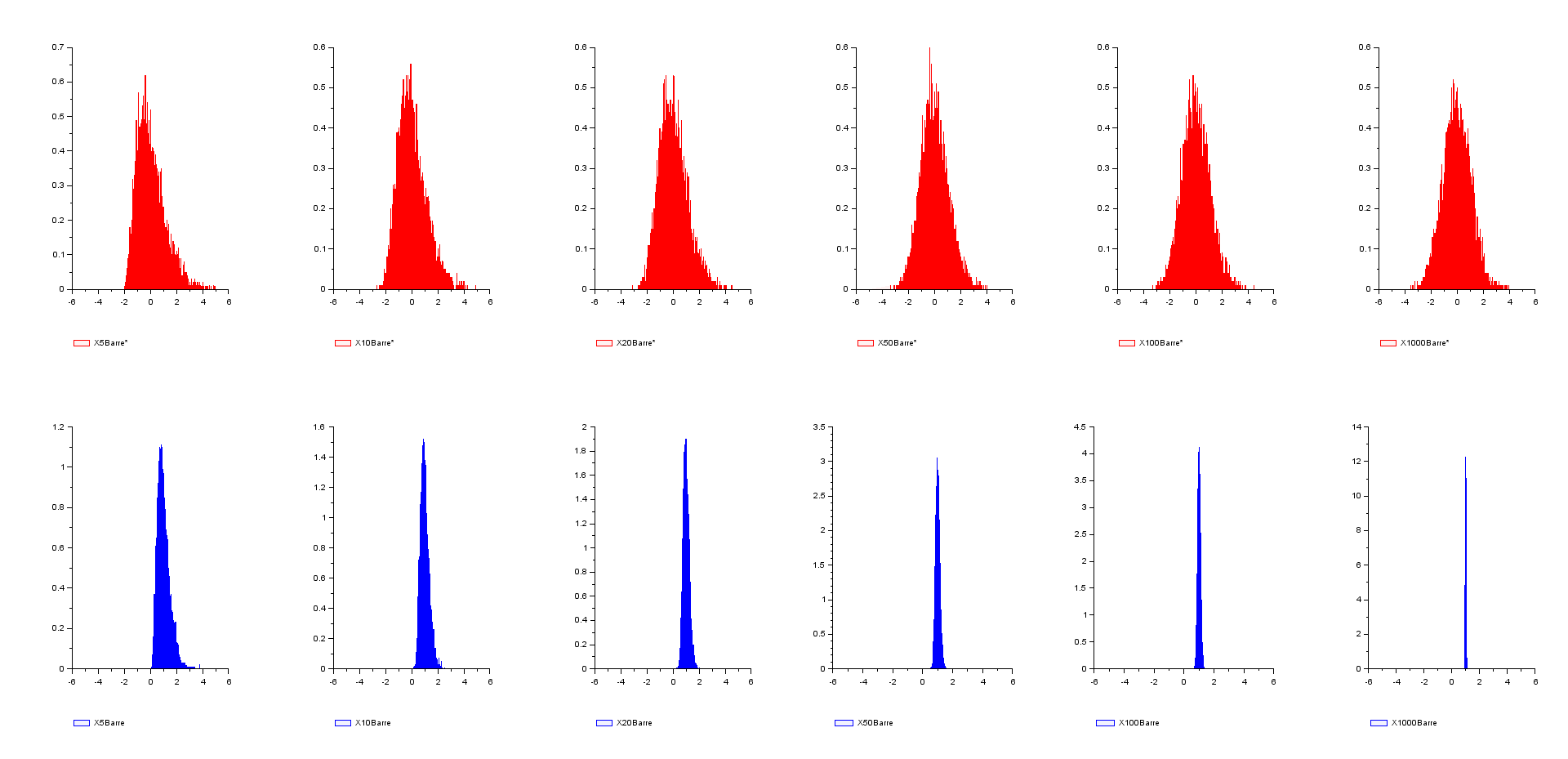
Exemples
- Soit $p\in\left]0,1\right[$. On considère une succession infinie de lancers d'une pièce dont la probabilité d'apparition de son côté pile est $p$ à chaque lancer. On note $X_{k}$ le résultat du lancer numéro $k$ : 0 si le côté face est obtenu, 1 si le côté pile est obtenu. On note $\ds\bar{X}_{n}=\frac{1}{n}\left(X_{1}+\dots+X_{n}\right)$ pour tout entier $n\geqslant1$.
- Justifier que : $$\ds\bar{X}_{n}\xrightarrow{\mathcal{P}}p$$
- Justifier que : $$\ds\frac{\bar{X}_{n}-p}{\sqrt{\frac{p(1-p)}{n}}}\xrightarrow{\mathcal{L}}X$$ avec $X\hookrightarrow\mathcal{N}(0,1)$.
- On pose : $$\ds Y_{n}\hookrightarrow\mathcal{N}\left(p,\frac{p(1-p)}{n}\right)$$ pour tout $n\geqslant1$. Justifier que, pour $n$ « assez grand », on a : $$\ds\forall\alpha\in\left]0,p\right[,\;\mathbb{P}\left(\bar{X}_{n}\in[p-\alpha,p+\alpha]\right)\approx\mathbb{P}\left(Y_{n}\in[p-\alpha,p+\alpha]\right)$$
- Soit $(X_{n})_{n\geqslant1}$ une suite de variables aléatoires mutuellement indépendantes suivant toutes une même loi dont on ne connaît que l'espérance $\mu$ et la variance $\sigma^{2}\neq0$. Soit $S_{n}=X_{1}+\dots+X_{n}$ pour tout $n\geqslant1$. Soit $N_{n}\hookrightarrow\mathcal{N}(n\mu,n\sigma^{2})$. Justifier que, pour tout intervalle $I$ de $\R$ et tout entier $n$ « assez grand », on a : $$\ds\mathbb{P}\left(S_{n}\in I\right)\approx\mathbb{P}\left(N_{n}\in I\right)$$
<html><a name=“approximation_loi_binomiale_par_loi_normale”></a></html>
Théorème : Approximation 2
- Soit $p\in\left]0,1\right[$. On suppose que $X_{n}\hookrightarrow\mathcal{B}(n,p)$ pour tout entier $n\geqslant1$ et on note $X_{n}^{*}$ sa variable centrée réduite associée. Soit $N\hookrightarrow\mathcal{N}(0,1)$. Alors : $$\ds X_{n}^{*}\xrightarrow{\mathcal{L}}N$$
- Approximation d'une loi binomiale par une loi normale.
En pratique, dès lors que : $$\boxed{n\geqslant30}\qquad\boxed{np\geqslant15}\qquad\boxed{n(1-p)\geqslant5}$$ on peut approcher la loi $\mathcal{B}(n,p)$ par la loi $\mathcal{N}\left(np,np(1-p)\right)$.
<html><a name=“approximation_loi_poisson_par_loi_normale”></a></html>
Théorème : Approximation 3
- On suppose que $X_{n}\hookrightarrow\mathcal{P}(n)$ pour tout entier $n\geqslant1$ et on note $X_{n}^{*}$ sa variable centrée réduite associée. Soit $N\hookrightarrow\mathcal{N}(0,1)$. Alors : $$\ds X_{n}^{*}\xrightarrow{\mathcal{L}}N$$
- Approximation d'une loi Poisson par une loi normale.
En pratique, dès lors que : $$\boxed{\lambda\geqslant20}$$on peut approcher la loi $\mathcal{P}(\lambda)$ par la loi $\mathcal{N}\left(\lambda,\lambda\right)$.
Exemple
Un pisciculteur possède, dans un même bassin, 3000 saumons et 7000 truites. Il attrape successivement et avec remise 100 poissons. Soit $X$ le nombre de saumons pêchés. En procédant à une approximation successive, déterminer une valeur approchée de $\mathbb{P}\left(20\leqslant X\leqslant40\right)$.
