Table des matières
Convergence en probabilité
Inégalités probabilistes
<html><a name=“markov”></a></html>
Théorème : Inégalités de Markov et de Bienaymé-Tchebychev
Soit $X$ une variable aléatoire discrète ou à densité.
- Inégalité de Markov
Si $X$ est à valeurs positives et admet une espérance alors :
$$\ds\forall a\in\left]0,+\infty\right[,\;\mathbb{P}(X\geqslant a)\leqslant\frac{\mathbb{E}(X)}{a}$$ - Corollaire : Soit $r\in\left]0,+\infty\right[$. Si $|X|^{r}$ admet une espérance alors :
$$\ds\forall a\in\left]0,+\infty\right[,\;\mathbb{P}(|X|\geqslant a)\leqslant\frac{\mathbb{E}(|X|^{r})}{a^{r}}$$En particulier, si $X$ admet un moment d'ordre 2, alors :
$$\ds\forall a\in\left]0,+\infty\right[,\;\mathbb{P}(|X|\geqslant a)\leqslant\frac{\mathbb{E}\left(X^{2}\right)}{a^{2}}$$ - Inégalité de Bienaymé-Tchebychev
Si $X$ admet une variance alors :
$$\ds\forall a\in\left]0,+\infty\right[,\;\mathbb{P}(\left|X-\mathbb{E}(X)\right|\geqslant a)\leqslant\frac{\mathbb{V}(X)}{a^{2}}$$
Remarque
Le caractère très général (valable pour tout type de lois, qu'elles soient discrètes ou à densité ou ni l'un ni l'autre) de ces inégalités les rend particulièrement peu précises. Comparer ainsi les inégalités de Markov et Bienaymé-Tchebychev pour $X\hookrightarrow\mathcal{U}([0,1])$ avec $a>1$ puis pour $\ds X\hookrightarrow\mathcal{G}\left(\frac{2}{3}\right)$ avec $a>100$.
Définition et propriétés
Définition
On dit que la suite de variables aléatoires $(X_{n})_{n\in\N}$ converge en probabilité vers la variable aléatoire $X$ et on note $X_{n}\xrightarrow{\mathcal{P}}X$ si et seulement si :
$$\ds\forall\varepsilon>0,\;\lim_{n\to+\infty}{\mathbb{P}\left(|X_{n}-X|>\varepsilon\right)}=0$$
Remarques
- Cette définition de la convergence en probabilité est évidemment équivalente à :
$$\ds\forall\varepsilon>0,\;\lim_{n\to+\infty}{\mathbb{P}\left(|X_{n}-X|\leqslant\varepsilon\right)}=1$$ - Une interprétation de cette définition est de dire que la variable aléatoire $X_{n}$ ne peut presque sûrement pas prendre des valeurs très différentes de celles de $X$ lorsque $n$ tend vers l'infini. Par contre, rien n'oblige à ce que $X_{n}(\omega)$ soit « proche » de $X(\omega)$ pour chaque éventualité $\omega$.
- Dans la notation $X_{n}\xrightarrow{\mathcal{P}}X$, la notion de $n$ tend vers l'infini est sous-entendue. On rencontre parfois la notation :
$$\ds X_{n}\xrightarrow[n\to+\infty]{\mathcal{P}}X$$
Exemples
- Soit $p\in\left]0,1\right[$, $X=p1\!\!1_{\Omega}$ (variable aléatoire certaine prenant la valeur $p$) et, pour tout entier naturel $n$ non nul :
$$\ds X_{n}\hookrightarrow\mathcal{B}(n,p)$$En utilisant l'inégalité de Bienaymé-Tchebychev, montrer que :
$$\ds\frac{1}{n}X_{n}\xrightarrow{\mathcal{P}}X$$Interprétation numérique :
epsilon=input("epsilon=") ; m=10000 p=rand() ; Z=zeros(1,m) for n=[10,100,1000,10000,100000] X=grand(1,m,"bin",n,p)/n pr=length(find(abs(X-p)>epsilon))/m disp(pr) end
Résultat d'une exécution du script :
epsilon=0.01 1. 0.829 0.5027 0.0322 0. - Soit $U\hookrightarrow\mathcal{U}([0,1])$ et $(X_{n})_{n\geqslant1}$ une suite de variables aléatoires mutuellement indépendantes ayant toutes la même loi que $U$. Pour tout entier naturel $n$ non nul, on pose :
$$I_{n}=\inf(X_{1},\dots,X_{n})$$$$S_{n}=\sup(X_{1},\dots,X_{n})$$ - - Calculer $\mathbb{P}\left(|S_{n}-1|>\varepsilon\right)$ pour tout entier $n\geqslant1$ et tout réel $\varepsilon>0$.- En déduire que $S_{n}\xrightarrow{\mathcal{P}}1\!\!1_{\Omega}$.
- Montrer que la suite $(I_{n})$ converge en probabilité vers une variable certaine que l'on précisera.
- Pour tout entier $n\geqslant1$, on définit $X_{n}$ par :
$$\ds X_{n}(\Omega)=\{0,n\},\qquad\mathbb{P}\left(X_{n}=0\right)=1-\frac{1}{n},\qquad\mathbb{P}\left(X_{n}=n\right)=\frac{1}{n}$$- Montrer que $(X_{n})$ converge en probabilité vers la variable certaine égale à 0.
- Comparer $\ds\lim_{n\to+\infty}{\mathbb{E}(X_{n})}$ avec $\mathbb{E}(01\!\!1_{\Omega})$.
- On suppose que $\Omega$ est l'intervalle $[0,1]$, $\mathcal{B}$ est la tribu des boréliens de $[0,1]$ (intersections des boréliens de $\R$ avec $[0,1]$) et $\mathbb{P}$ est la probabilité uniforme. Soit $X$ la variable certaine égale à 0. Pour tout entier naturel $n$, on pose :
$$\ds X_{n}=1\!\!1_{\left[0,\frac{1}{n+1}\right]}$$Montrer que $X_{n}\xrightarrow{\mathcal{P}}X$.
Remarques
- Il n'y a pas unicité de la limite lors de la convergence en probabilité, plus précisément :
$$\ds \begin{cases} X_{n} & \xrightarrow{\mathcal{P}}X \\ X_{n} & \xrightarrow{\mathcal{P}}X' \end{cases}\quad\implies\quad\mathbb{P}\left(X\ne X'\right)=0$$(les variables $X$ et $X'$ sont presque sûrement égales pour la probabilité $\mathbb{P}$).
Vérifier, dans l'exemple ci-avant, que l'on a aussi :
$$\ds X_{n}\xrightarrow{\mathcal{P}}1\!\!1_{\{0\}}$$ - On ne peut pas composer la convergence en probabilité avec l'espérance (cf un exemple ci-dessus).
Théorème (admis)
Si $X_{n}\xrightarrow{\mathcal{P}}X$ et si $f\colon\R\to\R$ est continue sur $\R$ alors $f(X_{n})\xrightarrow{\mathcal{P}}f(X)$.
Exemple
- Démontrer le théorème dans le cas particulier où la fonction $f$ est continue sur un intervalle $I$ et où $X$ est la variable certaine égale à un réel $\lambda$ élément de $I$.
- En déduire que si $X_{n}\xrightarrow{\mathcal{P}}\lambda$ avec $\lambda>0$ alors $\ds\frac{1}{X_{n}}\xrightarrow{\mathcal{P}}\frac{1}{\lambda}$ et $\sqrt{X_{n}}\xrightarrow{\mathcal{P}}\sqrt{\lambda}$.
Loi faible des grands nombres
Introduction
On lance une pièce de monnaie une infinité de fois. À chaque lancer, la probabilité d'apparition de son côté pile est $p$ où $0<p<1$, inconnu a priori. Déterminer le nombre $n$ de lancers à effectuer pour que la fréquence d'apparition de pile soit une valeur approchée de $p$ à $10^{-8}$ près avec une probabilité d'au moins 0,99. Que cela change-t-il si on sait que $p=0,1$ ?
<html><a name=“loi_faible_grands_nombres”></a></html>
Théorème : Loi faible des grands nombres
Soit $m\in\R$ et $\sigma\in\R^{+}$. On suppose que les $X_{n}$ sont mutuellement indépendantes (ou même seulement deux à deux non corrélées dans le cas discret), admettent toutes le réel $m$ pour espérance et le réel $\sigma^{2}$ pour variance. Alors :
$$\ds\frac{1}{n}(X_{1}+\dots+X_{n})\xrightarrow{\mathcal{P}}m1\!\!1_{\Omega}$$
p=input("Donner p : ") q=1-p i=0 for n=[1,2,5,10,20,50,100,200,500] i=i+1 subplot(3,3,i) plot2d([-0.5,0],[0,0],5) plot2d([1,1.5],[1,1],5) x=[0:1/n:1] S=[0:n] liste_nb_tirages=n*ones(x) liste_proba_succes=p*ones(x) liste_proba_echec=q*ones(x) [P,Q]=cdfbin("PQ",S,liste_nb_tirages,liste_proba_succes,liste_proba_echec) for k=[1:n] plot2d([x(k),x(k+1)],[P(k),P(k)],5) end end
Avec des lois de Bernoulli de paramètre p=0.3
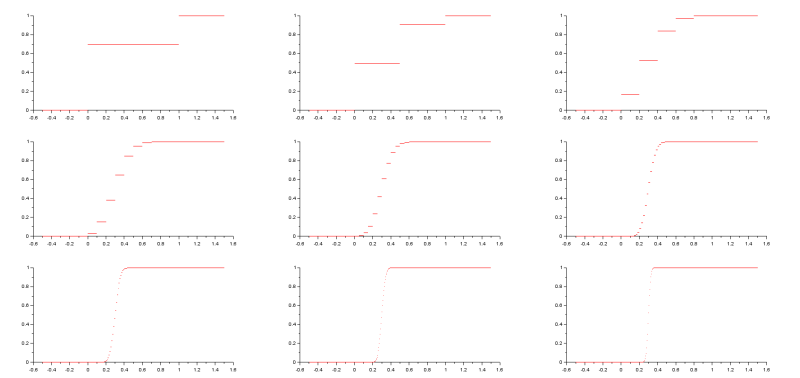
Exemple
On définit une suite de variables aléatoires indépendantes $(X_{n})_{n\geqslant1}$ sur le même espace probabilisé par : $$\ds\forall n\in\N^{*},\; X_{n}\hookrightarrow\mathcal{E}(1)$$ Montrer de deux façons différentes que la suite $(\bar{X}_{n})_{n\geqslant1}$, définie par $\ds\bar{X}_{n}=\frac{1}{n}\sum_{k=1}^{n}{X_{k}}$, converge en probabilité vers une variable aléatoire que l'on précisera.
Remarques
- Ce théorème doit nous conforter dans notre intuition et dans notre choix de la définition de la probabilité d'un événement comme fréquence limite de son nombre d'apparitions lors d'une succession infinie de réalisations indépendantes de l'expérience aléatoire sous-jacente.
- Ce théorème sert de base à l'estimation de la valeur du réel $m$ lorsqu'il est inconnu (méthodes dites de Monte Carlo), notamment lors de simulations informatiques.