Intégrales généralisées ou intégrales impropres
Définition : Intégrale généralisée
- On suppose que $f$ est définie et continue sur $\left[a,b\right[$ (resp. $\left]a,b\right]$) avec $a\in\R$ et $b\in\left]a,+\infty\right[\cup\{+\infty\}$ (resp. $b\in\R$ et $a\in\left]-\infty,b\right[\cup\{-\infty\}$).
- L'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ est qualifiée d'impropre en la borne $b$ (resp en la borne $a$).
- On dit que $f$ admet une intégrale sur l'intervalle $\left[a,b\right[$ (resp. $\left]a,b\right]$) ou bien que l'intégrale (qualifiée aussi de généralisée) $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ est convergente en la borne $b$ (resp. en la borne $a$) si et seulement si : $$\ds\lim_{\substack{x\to b\\ x<b}}{\int_{a}^{x}{f(t)\mathrm{d} t}}\in\R$$ resp. $$\ds\lim_{\substack{x\to a\\ x>a}}{\int_{x}^{b}{f(t)\mathrm{d} t}}\in\R$$ et la valeur de l'intégrale se note alors : $$\ds\int_{a}^{b}{f(t)\mathrm{d} t}=\lim_{x\to b}{\int_{a}^{x}{f(t)\mathrm{d} t}}$$ resp. $$\ds\int_{a}^{b}{f(t)\mathrm{d} t}=\lim_{x\to a}{\int_{x}^{b}{f(t)\mathrm{d} t}}$$
- L'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$, impropre en $b$ (resp. $a$), est dite divergente si et seulement si elle ne converge pas en $b$ (resp. $a$), la limite pouvant être infinie ou bien ne pas exister.
- Soit $(a,b)\in\bar{\R}^{2}$ tel que $a<b$. Soit $c\in\left]a,b\right[$. On suppose que $f$ est définie et continue sur $\left]a,b\right[$.
- L'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ est qualifiée d'impropre en les deux bornes $a$ et $b$.
- On dit que $f$ admet une intégrale sur l'intervalle $]a,b[$ ou bien que l'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ est convergente en les deux bornes $a$ et $b$ si et seulement si les deux intégrales impropres $\ds\int_{a}^{c}{f(t)\mathrm{d} t}$ et $\ds\int_{c}^{b}{f(t)\mathrm{d} t}$ sont convergentes et on note :
$$\ds\int_{a}^{b}{f(t)\mathrm{d} t}=\int_{a}^{c}{f(t)\mathrm{d} t}+\int_{c}^{b}{f(t)\mathrm{d} t}=\lim_{x\to a}{\int_{x}^{c}{f(t)\mathrm{d} t}}+\lim_{x\to b}{\int_{c}^{x}{f(t)\mathrm{d} t}}$$ - L'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$, impropre en $a$ et en $b$, est divergente si et seulement si elle est divergente en $a$ ou en $b$.
Exemples
- Montrer que les intégrales suivantes convergent et préciser leur valeur : $$\ds\int_{0}^{+\infty}{\mathrm{e}^{-x}\mathrm{d} x}$$ $$\ds\int_{\mathrm{e}}^{+\infty}{\frac{\mathrm{d} x}{x\ln^{2}(x)}}$$ $$\ds\int_{-\infty}^{-1}{\frac{\mathrm{d} x}{x^{10}}}$$ $$\ds\int_{-1}^{1}{\frac{\mathrm{d} t}{\sqrt{1-t^{2}}}}$$ $$\ds\int_{0}^{1}{\ln(t)\mathrm{d} t}$$
- Montrer que les intégrales qui suivent sont divergentes : $$\ds\int_{0}^{1}{\frac{\mathrm{d} x}{x}}$$ $$\ds\int_{1}^{+\infty}{\frac{\mathrm{d} x}{x}}$$ $$\ds\int_{\mathrm{e}}^{+\infty}{\frac{\mathrm{d} x}{x\ln(x)}}$$ $$\ds\int_{-1}^{1}{\frac{\mathrm{d} t}{1-t^{2}}}$$
Remarques
- La plupart des énoncés qui suivent seront uniquement énoncés dans le cadre d'intégrales impropres en la borne « supérieure » de l'intégrale (mais s'énoncent de manière évidente dans les deux autres cas).
- Si l'intégrale impropre $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ converge alors on convient que l'intégrale $\ds\int_{b}^{a}{f(t)\mathrm{d} t}$ converge et que : $$\ds\int_{b}^{a}{f(t)\mathrm{d} t}=-\int_{a}^{b}{f(t)\mathrm{d} t}$$
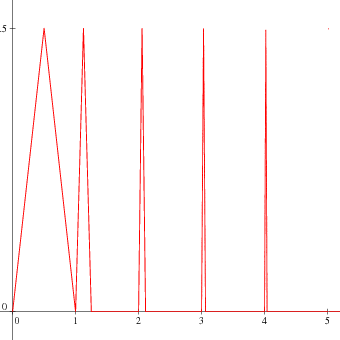
- On sait que, si une série converge, alors son terme général converge vers 0 : CE N'EST PAS LE CAS POUR LES INTÉGRALES IMPROPRES comme le prouve la fonction $f$ définie sur $[0,+\infty[$ par : $$\ds\forall n\in\N,\;\forall x\in[n,n+1[,\; f(x)=\left\{ \begin{array}{ll} (n+1)^{2}(x-n) & \text{si}\; x\in\left[n,n+\frac{1}{2(n+1)^{2}}\right[\\ (n+1)^{2}\left(n+\frac{1}{(n+1)^{2}}-x\right) & \text{si}\; x\in\left[n+\frac{1}{2(n+1)^{2}},n+\frac{1}{(n+1)^{2}}\right[\\ 0 & \text{si}\; x\in\left[n+\frac{1}{(n+1)^{2}},n+1\right[ \end{array}\right.$$ puisque $\ds f\left(n+\frac{1}{2(n+1)^{2}}\right)=\frac{1}{2}$ pour tout entier $n\geqslant0$ et $\ds\int_{0}^{+\infty}{f(t)\mathrm{d} t}=\sum_{n=0}^{+\infty}{\frac{1}{2(n+1)^{2}}}$ est convergente.
Théorème : Intégrale faussement impropre
Si $f$ n'est pas définie en $b\in\R$ mais est prolongeable par continuité en $b$ (fonction notée alors $\tilde{f}$) alors l'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ converge et : $$\ds\int_{a}^{b}{f(t)\mathrm{d} t}=\int_{a}^{b}{\tilde{f}(t)\mathrm{d} t}$$
Exemple
Montrer que les intégrales $\ds\int_{0}^{1}{\frac{\ln(1-x)}{x}\mathrm{d} x}$ et $\ds\int_{0}^{1}{t\ln(t)\mathrm{d} t}$ convergent. Les calculer si possible.
Définition : Intégrale d'une fonction avec points de discontinuité
Soit $(a,b)\in\bar{\R}^{2}$ tel que $a<b$. On suppose que $f$ est continue sur $\left]a,b\right[$ sauf en un nombre finis de points $a_{1},\dots,a_{n}$ tels que : $$a=a_{0}<a_{1}<\dots<a_{n}<b=a_{n+1}$$On dit que $f$ admet une intégrale $]a,b[$ ou bien que l'intégrale $\ds\int_{a}^{b}{f(t)\mathrm{d} t}$ converge si et seulement si, pour tout $i\in\llbracket0,n\rrbracket$, l'intégrale $\ds\int_{a_{i}}^{a_{i+1}}{f(t)\mathrm{d} t}$, impropre en les deux bornes $a_{i}$ et $a_{i+1}$, est convergente. En cas de convergence, on a : $$\ds\int_{a}^{b}{f(t)\mathrm{d} t}=\sum_{i=0}^{n}{\int_{a_{i}}^{a_{i+1}}{f(t)\mathrm{d} t}}$$
Exemples
- Existence et valeur éventuelle de $\ds\int_{-\infty}^{+\infty}{f(t)\mathrm{d} t}$ lorsque $f(t)=\begin{cases} \mathrm{e}^{t} & \text{si}\; t\leqslant0\\ \ds\frac{1}{\sqrt{t}} & \text{si}\; t\in\left]0,3\right]\\ \ds\frac{1}{(t-2)^{2}} & \text{si}\; t>3 \end{cases}$.
- Existence et valeur éventuelle de l'intégrale $\ds\int_{-1}^{1}{\frac{\mathrm{d} x}{\sqrt[3]{x^{2}}}}$.
Théorème : Primitives et intégrales
- Soit $a\in\R\cup\{-\infty\}$. On suppose que $f$ est continue sur $\left]a,+\infty\right[$ (resp. $\left]a,b\right]$ avec $b\in\left]a,+\infty\right[$) et que $\ds\int_{a}^{x_{0}}{f(t)\mathrm{d} t}$, impropre en $a$, converge pour un certain $x_{0}\in\left]a,+\infty\right[$ (resp. $\left]a,b\right]$). Alors :
- l'intégrale $\ds\int_{a}^{x}{f(t)\mathrm{d} t}$ est définie pour tout réel $x\in\left]a,+\infty\right[$ (resp. $x\in\left]a,b\right]$),
- la fonction $\ds F\colon x\mapsto\int_{a}^{x}{f(t)\mathrm{d} t}$ est de classe $\mathcal{C}^1$ sur $\left]a,+\infty\right[$ (resp. $\left]a,b\right]$) et : $$\ds\forall x\in\left]a,+\infty\right[\;(\textrm{resp.}\;]a,b]),\; F'(x)=f(x)$$c'est à dire que $F$ est la primitive de $f$ sur $\left]a,+\infty\right[$ (resp. $]a,b]$) qui admet 0 pour limite en $a$.
- Soit $b\in\R\cup\{+\infty\}$. On suppose que $f$ est continue sur $\left]-\infty,b\right[$ (resp. $\left[a,b\right[$ avec $a\in\left]-\infty,b\right[$) et que $\ds\int_{x_{0}}^{b}{f(t)\mathrm{d} t}$ converge pour un certain $x_{0}\in\left]-\infty,b\right[$ (resp. $\left[a,b\right[$). Alors :
- l'intégrale $\ds\int_{x}^{b}{f(t)\mathrm{d} t}$ est définie pour tout réel $x\in\left]-\infty,b\right[$ (resp. $x\in\left[a,b\right[$),
- la fonction $\ds F\colon x\mapsto\int_{x}^{b}{f(t)\mathrm{d} t}$ est de classe $\mathcal{C}^1$ sur $\left]-\infty,b\right[$ (resp. $\left[a,b\right[$) et :
$$\ds\forall x\in\left]-\infty,b\right[\;(\textrm{resp.}\;[a,b[),\; F'(x)=-f(x)$$c'est à dire que $F$ est la primitive de $-f$ sur $\left]-\infty,b\right[$ (resp. $\left[a,b\right[$) qui admet 0 pour limite en $b$.
Exemple
Étudier la fonction $\ds G\colon x\mapsto\int_{x}^{+\infty}{\mathrm{e}^{-t^{2}}\mathrm{d} t}$.
