Ajustement affine

<html

<a name=“moindres_carres”></a></html>Théorème : Méthode des moindre carrés> La droite d'équation :
$$y-\bar{Y}=\dfrac{\text{Cov}(X,Y)}{\sigma(X)^{2}}(x-\bar{X})$$ passe par le point moyen et est la droite d'équation réduite de la forme $y=ax+b$ qui minimise la somme :
$$\ds\sum_{i=1}^{n}{f_{i}(ax_{i}+b-y_{i})^{2}}$$ pour $(a,b)\in\mathbb{R}^{2}$. Autrement dit :
$$a=\dfrac{\text{Cov}(X,Y)}{\sigma(X)^{2}}\qquad\text{et}\qquad b=\bar{Y}-\bar{X}\dfrac{\text{Cov}(X,Y)}{\sigma(X)^{2}}$$ réalisent ce minimum sur $\mathbb{R}^{2}$.

<html

<a name=“ajustement”></a></html>Définition : Droite d'ajustement>

La droite définie ci-dessus est appelée droite d'ajustement (ou droite de régression) de $\boldsymbol{Y}$ en $\boldsymbol{X}$.
La somme $\ds\sum_{i=1}^{n}{f_{i}(ax_{i}+b-y_{i})^{2}}$ est appelée résidu quadratique.

Remarques

La droite d'équation $x-\bar{X}=\dfrac{\text{Cov}(X,Y)}{\sigma(Y)^{2}}(y-\bar{Y})$ minimise la somme $\ds\sum_{i=1}^{n}{f_{i}(ay_{i}+b-x_{i})^{2}}$ et s'appelle droite d'ajustement de $X$ en $Y$.
Notons $Z=(1,\dots,1)$ le caractère constant égal à 1 sur la population commune à $X$ et à $Y$. Ajuster $Y$ en $X$ revient à considérer le projeté orthogonal de $Y$ sur le sous espace $\Vect(X,Z)$ de l'espace euclidien $\R^{n}$ pour le produit scalaire canonique.
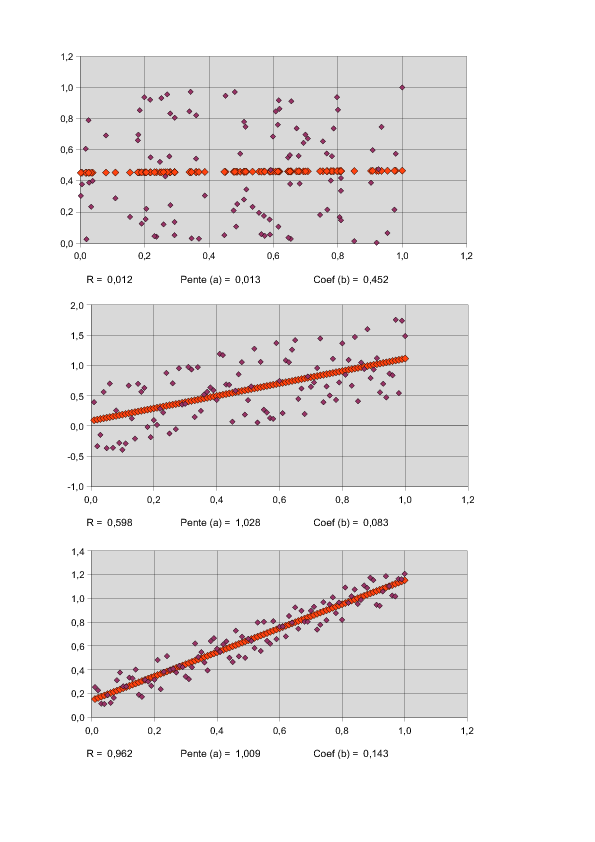
Lorsque $|r|=|\rho(X,Y)|>0.9$ (valeur dépendant des auteurs et des besoins), on considère que l'ajustement affine de $Y$ en $X$ est satisfaisant (sinon, il faut déterminer un autre type d'ajustement).

Accueil