Étude d'une série statistique

L'objectif de ce paragraphe est de dégager des valeurs caractéristiques les plus pertinentes possibles d'une série statistique afin réduire son étude au calcul de quelques nombres.

Toutes les séries statistiques $(\Omega,E,X)$ sont telles que l'ensemble $E$ est une partie de $\mathbb R$, c'est à dire que $X$ est un caractère quantitatif.

Notions de fréquences

<html

<a name=“frequence”></a></html>Définitions : Différents types de fréquences>

Fréquence : Si $F$ est une partie de $E$ alors la fréquence de $F$ pour le caractère $X$ est le quotient :$$ \dfrac{\text{Card}(X^{-1}(F))}{\text{Card}(\Omega)}$$
- Fréquences cumulées croissantes : Si $x$ est une modalité de $X$ alors la fréquence cumulée croissante en $x$ est la somme :$$\ds\sum_{\substack{t\in X(\Omega)\\ t\leqslant x}}{\frac{\text{Card}(X^{-1}(\{t\}))}{\text{Card}(\Omega)}}$$
- Fréquences cumulées décroissantes : Si $x$ est une modalité de $X$ alors la fréquence cumulée décroissante en $x$ est la somme :$$\ds\sum_{\substack{t\in X(\Omega)\\ t\geqslant x}}{\frac{\text{Card}(X^{-1}(\{t\}))}{\text{Card}(\Omega)}}$$
On représente ces deux diagrammes des effectifs cumulés croissants et décroissants sous la forme :
- cas discret : histogrammes,
- cas continu : lignes polygonales.

Exemple 1
Le nombre d'interventions graves quotidiennes, relevées dans un cabinet vétérinaire pour une année donnée, est indiqué dans le tableau ci-dessous :

Interventions	0	1	2	3	4	5	6	Total
Effectif	84	105	72	59	28	15	2	365

Exemple 2
Voici un relevé de la taille d'un certain nombre de personnes :

Taille	[155,160[	[160,165[	[165,170[	[170,175[	[175,180[	[180,185[	Total
Effectif	3	7	9	16	11	4	50

Paramètres de positions

<html

<a name=“position”></a></html>Définitions : Paramètres de position>

Mode : On appelle mode de $X$ toute modalité d'effectif maximal.
Moyenne :
- Cas discret: ${\displaystyle \bar{X}=\sum_{x\in X(\Omega)}{\frac{x\times\text{Card}(X^{-1}(\{x\}))}{\text{Card}(\Omega)}}}$.
- Cas continu: même principe en utilisant les classes (pour chaque classe, on utilise son centre $x$ et son effectif).
Médiane et quartiles :
- Cas discret: La médiane (resp. le premier quartile, le troisième quartile) est une valeur $M$ (resp. $Q_{1}$, $Q_{3}$) telle que 50% (resp. 25%, 75%) des valeurs de $X$ lui sont inférieures ou égales et 50% (resp. 75%, 25%) lui sont supérieures ou égales.
- Cas continu : même principe en utilisant les classes (recherche graphique ou par calcul).
Déciles et centiles : même principe que les quartiles en partageant en 10 ou en 100 au lieu de 4.

Remarques

Selon les ouvrages (et donc les auteurs), “la” définition de “la” médiane peut varier !
La médiane est le deuxième quartile.
On représente graphiquement ces notion à l'aide de diagrammes en boîtes à moustache.

Exemples
Calculer les moyennes dans les deux exemples qui précèdent (vétérinaire et taille).

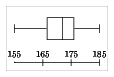
Paramètres de dispersion

<html

<a name=“dispersion”></a></html>Définitions : Paramètres de dispersion>

Étendue : c'est la différence entre la modalité maximale et la modalité minimale, c'est à dire le réel $$ e=\max X(\Omega)-\min X(\Omega)$$L'intervalle $\left[\min X(\Omega),\max X(\Omega)\right]$ contient 100% des effectifs.
Intervalle inter-quartiles : c'est l'intervalle $[Q_{1},Q_{3}]$, qui contient donc 50% des effectifs.
Écart moyen : la moyenne des écarts absolus à la moyenne, c'est à dire le réel
$$\ds\mu=\frac{1}{\text{Card}(\Omega)}\sum_{x\in X(\Omega)}{\text{Card}(X^{-1}(\{x\}))\times\left|x-\bar{X}\right|}$$On utilise, bien sûr, le milieu de classe dans le cas continu.
Variance : c'est le réel
$$\ds\mathbb V(X)=\frac{1}{\text{Card}(\Omega)}\sum_{x\in X(\Omega)}{\text{Card}(X^{-1}(\{x\}))\times\left(x-\bar{X}\right)^{2}}$$
Écart type : c'est le réel $\sigma(X)=\sqrt{\mathbb V(X)}$.

Exemples Calculer les différents paramètres de dispersion dans les deux exemples qui précèdent.

Théorème : Propriétés

Les règles de calculs sur les espérances/variances/écarts-type des variables aléatoires ainsi que leurs propriétés s'appliquent aux moyennes/variances/écart-type des séries statistiques.

Remarque Pour une répartition «normale» (dans un sens défini plus tard), l'intervalle :

$\left[\bar{X}-\sigma(X),\bar{X}+\sigma(X)\right]$ contient environ 68% des effectifs,
$\left[\bar{X}-2\sigma(X),\bar{X}+2\sigma(X)\right]$ contient environ 95% des effectifs,
$\left[\bar{X}-3\sigma(X),\bar{X}+3\sigma(X)\right]$ contient environ 99% des effectifs.

Sommaire du chapitre 1

Maths en ECS2

Index

Forum maths

Accueil