Introduction

1. Voici les résultats de 100 réalisations d'une certaine loi de Poisson $\mathcal{P}(\lambda)$ où $\lambda$ est inconnu :
   $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline 21 & 27 & 13 & 20 & 20 & 23 & 23 & 12 & 19 & 23 & 18 & 15 & 17 & 18 & 27 & 28 & 21 & 18 & 14 & 18 \\ \hline 20 & 16 & 28 & 23 & 12 & 16 & 15 & 22 & 18 & 23 & 25 & 17 & 17 & 21 & 17 & 19 & 15 & 22 & 18 & 14 \\ \hline 20 & 23 & 18 & 21 & 19 & 14 & 17 & 23 & 20 & 28 & 27 & 16 & 20 & 22 & 21 & 21 & 19 & 14 & 18 & 23 \\ \hline 12 & 22 & 22 & 16 & 18 & 17 & 22 & 21 & 22 & 23 & 32 & 23 & 18 & 17 & 15 & 14 & 13 & 14 & 22 & 17 \\ \hline 22 & 24 & 24 & 21 & 22 & 17 & 19 & 17 & 25 & 11 & 18 & 14 & 15 & 16 & 24 & 25 & 19 & 15 & 21 & 27 \\ \hline \end{array}$$ On visualise les résultats sous la forme d'un histogramme des fréquences :
   
   

   lambda=grand(1,1,"uin",10,100)
   X=grand(1,100,"poi",lambda)
   disp(mean(X))
   histplot(0.5+[-1:3*lambda],X)

   
   La valeur moyenne de cette série statistique est 19,53. On note $X_{1},\dots,X_{100}$ les variables aléatoires correspondant à ces 100 tirages et $x_{1},\dots,x_{100}$ les valeurs de ces 100 réalisations.

   1. On pose : $\ds f(\lambda)=\prod_{k=1}^{100}{\mathbb{P}\left(X_{k}=x_{k}\right)}$. Quelle valeur de $\lambda$ maximise la fonction $f$ ? On l'appelle maximum de vraisemblance puisque cela correspond à la « probabilité » la plus grande.
   2. On pose : $\ds \bar{X}_{n}=\frac{1}{n}\sum_{k=1}^{n}{X_{k}}$. Soit $\alpha\in\left]0,1\right[$ (appelé risque d'erreur). En utilisant l'inégalité de Bienaymé-Tchebychev, montrer que :
      $$\ds \mathbb{P}\left(\left(\sqrt{\bar{X}_{n}+\frac{1}{4n\alpha}}-\frac{1}{2\sqrt{n\alpha}}\right)^{2}\leqslant\lambda\leqslant\left(\sqrt{\bar{X}_{n}+\frac{1}{4n\alpha}}+\frac{1}{2\sqrt{n\alpha}}\right)^{2}\right)\geqslant1-\alpha$$En déduire un encadrement de $\lambda$ au risque 0.05 lorsque $n=100$.
2. On effectue 10000 nouvelles réalisations de cette loi $\mathcal{P}(\lambda)$. On visualise les résultats de la même loi avec 10000 nouvelles réalisations :
   
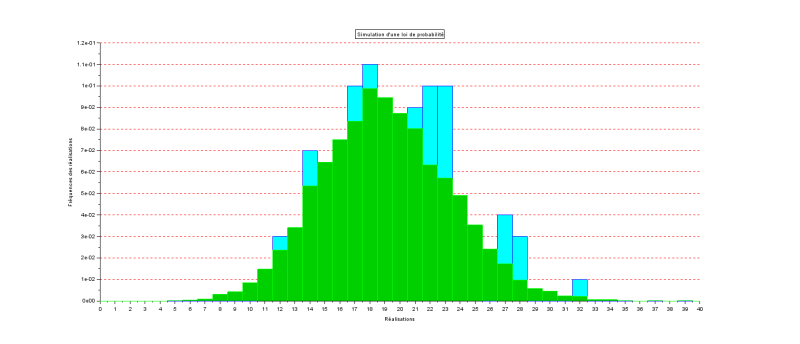
   La valeur moyenne de cette série statistique est 19.0333 et la variance est de 18.2622.
   1. Que donnent les deux résultats qui précèdent dans ce cas ?
   2. À l'aide du théorème de la limite centrée, en posant $\ds\Phi(t_{\alpha})=1-\frac{\alpha}{2}$, montrer que :
      $$\ds\mathbb{P}\left(\left(\sqrt{\bar{X}_{n}+\frac{t_{\alpha}^{2}}{4n}}-\frac{t_{\alpha}}{2\sqrt{n}}\right)^{2}\leqslant\lambda\leqslant\left(\sqrt{\bar{X}_{n}+\frac{t_{\alpha}^{2}}{4n}}+\frac{t_{\alpha}}{2\sqrt{n}}\right)^{2}\right)\geqslant1-\alpha$$En déduire un nouvel encadrement de $\lambda$ au risque 0.05 lorsque $n=10000$.

// estimation de n dans B(n,1/2) lorsque m->+oo
n=50 ; p=0.5 ; m=26
X=grand(1,m,"bin",n,p)
Y=2*mean(X)
disp([n,Y])
alpha=0.05 ; [P,Q]=cdfnor("X",0,1,1-alpha/2,alpha/2) ; t=P
disp([alpha,t])
a_TLC=Y+t^2/2/m-t/m*sqrt(Y+t^2/4/m)
b_TLC=Y+t^2/2/m+t/m*sqrt(Y+t^2/4/m)
disp([a_TLC,b_TLC])
a_IBT=Y+1/2/alpha/m-1/sqrt(alpha*m)*sqrt(Y+1/4/alpha/m)
b_IBT=Y+1/2/alpha/m+1/sqrt(alpha*m)*sqrt(Y+1/4/alpha/m)
disp([a_IBT,b_IBT])